

[Centro de recursos] [Formação] [Ateliers] [e-Revista] [moodle] [Início]
Ozarfaxinars
e-revista ISSN 1645-9180
Direção: Jorge Lima Edição e Coordenação: Fátima Pais
___71___
Julho 2017
Sendas de Sucesso
com o “método de Singapura” – Parte 2/3
Dárida Fernandes
Os resultados do PISA e do TIMSS têm provocado reflexões internas que nos ajudam a pensar mais sobre a educação e no modo como se aprende e ensina Matemática em idades elementares. Decorrente da minha experiência profissional de mais de trinta anos em diversos níveis de ensino, desde o 1.º Ciclo do Ensino Básico ao Ensino Superior, as minhas primeiras palavras são de agradecimento aos obreiros do sucesso nas salas de aula, que são os professores portugueses, ao conseguirem fazer a diferença e terem contribuído para uma melhoria significativa nos resultados do PISA e do TIMSS em Portugal durante estes últimos dez anos.

Dárida Maria Fernandes é Professora e Coordenadora da Unidade Técnico-Científica de Matemática, Ciências Naturais e Tecnologias da Escola Superior de Educação do Politécnico do Porto. Doutorada em Didática pela Universidade de Aveiro, Mestre em Educação na especialidade de Tecnologias de Informação pela Universidade do Minho. Licenciada em Matemática – Ramo Educacional pela Faculdade de Ciências da Universidade do Porto e Bacharel pela conclusão do Curso do Magistério Primário do Porto. Experiência profissional vasta no ensino da Matemática, desde o 1.º Ciclo do Ensino Básico (7 anos), no Ensino Básico e Secundário (3 anos) e no Ensino Superior (28 anos) relacionada com a formação de educadores e professores. Membro do Conselho Técnico-Científico por inerência de categoria profissional, desde 1989 e posteriormente por eleição, desde 2010, tendo assumido a responsabilidade de vários cargos de gestão intermédia na ESEPP. (Consultar nota curricular na íntegra)
“Ensinar é um exercício de imortalidade. De alguma forma continuamos a viver naqueles cujos olhos aprenderam a ver o mundo pela magia da nossa palavra. O professor, assim, não morre jamais...”
(Rubem Alves)
1. Introdução
Aprender e ensinar Matemática é uma experiência única pela relação que se estabelece com o estudante e com a disciplina. Necessariamente tem de ser um encontro intelectualmente estimulante que crie gosto e confiança entre o professor, o estudante e a classe. Neste processo deve existir alegria, bem-estar, intencionalidade e uma interação forte baseada no diálogo. O professor deve escutar atentamente o estudante para perceber o que está a pensar, mas também como está a relacionar os dados e os seus raciocínios, ativando mecanismos de metacognição. Esta comunicação é preciosa e é singular pela proximidade que se estabelece, procurando o professor desvendar as estratégias necessárias para ajudar a criança a desenvolver-se na sua plenitude, esclarecendo dúvidas, minorando bloqueios e, com uma atitude positiva, analisar formas de aprofundar conhecimento, valorizando ideias e raciocínios.
Por seu lado o estudante deve ter vontade expressa de aprender, revelando uma motivação intrínseca alicerçada num querer forte para pensar e agir, realizando com gosto os problemas e os exercícios propostos. Contudo, este querer quando não está alicerçado na família o papel do professor é ainda mais desafiante e útil (trata-se de uma causa pública que deveria ser cada vez mais valorizado numa sociedade democrática), pois é nestes contextos mais complexos que a ação do professor se torna absolutamente crucial! Se tal acontecer a criança ao ser estimulada, tem mais possibilidades de ter sucesso e isso faz crescer a sua vontade de aprender. Neste processo é necessário insistir na resolução de problemas e de exercícios para o estudante colocar perguntas, levantar hipóteses de resolução, conjeturar, redefinir novas estratégias, de modo a criar a autonomia e auto-estima nas suas aprendizagens matemáticas. Neste contexto educativo pró-ativo procura-se que a criança aprenda com motivação, de forma relacionada e compreendida a Matemática. Esta metodologia de trabalho concentra a criança no desenvolvimento de uma compreensão dos conceitos antes de se aprenderem as técnicas, utilizando uma abordagem visual e concreta que antecede a aprendizagem formal da matemática. Esta atitude fortalece a capacidade individual de interpretar a leitura de um problema e encoraja a descoberta de soluções.
Pelo que foi exposto, torna-se cada vez mais claro para mim, nesta experiência profissional de perto de quarenta anos no Ensino Primário e no Ensino Superior, relacionada com a pedagogia direta e com pesquisas nesta área, que o mais importante não é ensinar Matemática, mas é ensinar a aprender matemática. A atitude de aprender cria laços perenes com o conhecimento e esta postura faz a diferença na nossa vida e na vida das crianças e dos jovens que privam connosco. Por outro lado, esta motivação intrínseca de ambas as partes cria empatia, respeito e vontade de vencer. Eu acredito nestas premissas e o “Método de Singapura” vem ao encontro desta necessidade de termos uma atitude positiva para com a criança e o conhecimento, desenvolvendo crenças pedagógicas fortes sobre o ato de aprender e ensinar Matemática. Aliada e estas crenças, existe ainda, nesta cidade-estado de Singapura, uma organização política e social que valoriza a ação educativa do professor, uma ampla conceção curricular para um ensino eficaz, edificada numa estrutura com fundações pedagógicas internacionais de referência como Piaget, Dienes, Bruner, Skemp, Vygostky e Polya. Estas metodologias têm sido testadas, refinadas nos últimos 30 anos pela relação estreita com estudos atuais de neurocientistas e com a exploração didática de conceitos que fazem de Singapura um “laboratório de excelência no ensino da matemática”. Na parte II deste artigo sobre as sendas do “método de Singapura” serão abordados, como se referiu na primeira parte, os conceitos relacionados com “Number Bond”; “family facts numbers”; “Bar Model” e apresentadas as duas operações lineares: a adição e a subtração, nas suas diversas dimensões.
2. Noção de “Number Bond” (NB)
Nunca é de mais repetir que os novos conceitos matemáticos na Escola de Singapura têm de ser trabalhados seguindo a metodologia do Concrete Pictorial Abstract Approach (CPA). Por outro lado, têm de ser usados bons exemplos, com a exploração dos materiais mais adequados, antevendo a representação pictórica e, por fim, o registo simbólico. As lições e as atividades estão programadas para que o uso da resolução de problemas na exploração de qualquer tema seja uma forma de encorajar as crianças a pensarem a matemática ao mais alto nível, “matemática por mestria” (“maths for mastery”). O foco está no desenvolvimento de competências construídas naquilo que precisam de saber para aprofundar a compreensão relacional entre as matérias.
Convém ainda relembrar que na Escola de Singapura, a organização da classe é diferente e não se compadece com a disposição das mesas e cadeiras de forma tradicional. As questões e os exemplos explorados na Matemática são cuidadosamente concebidos por autores de referência que encorajam as crianças a pensar sobre matemática onde são desenvolvidos espaços de comunicação com a criança: em grupo, no “carpet time” (perto do professor e sentados no tapete ou em almofadas), no trabalho individualizado, em pares ou na classe. Raramente são propostas repetições mecânicas que não fazem sentido e os exemplos são explorados com o propósito de iniciar o estudo de um conceito e de o profundar de forma rigorosa e clara, evitando conceções erradas pré-concebidas.
Por outro lado, o uso de diagramas é estimulado e reconhecida a sua importância na resolução de problemas. O currículo de Singapura (2006, 2012) refere que os diagramas ajudam a contextualizar o problema e o esquema visual permite à criança compreender melhor a situação problemática. Conclui ainda que desenhar um diagrama é uma heurística poderosa no processo de resolução de problemas. È neste contexto programático e educativo que a noção de “Number Bond” e sua representação se sustenta. A figura 1 mostra a estrutura normalmente associada ao “Number Bond”, sendo concretizada com o exemplo da quantidade “5”.
Figura 1: Estrutura do “Number Bond” (NB) – todo-parte ou vice-versa.
Na exploração da noção de “NB” surgem várias situações. Por exemplo, na figura seguinte (figura 2) mostra-se o conceito de “Number Bond” relacionado com a “decomposição de um número em partes” trabalhado de forma lúdica, com uma exploração concretizada e simbólica de cada quantidade: do 6, 8 e 10. Os autores referem que, nestes casos, a variação da perceção encoraja a criança a estabelecer conexões entre as questões. Na imagem o número de berlindes aumenta de uma unidade, num dos copos, mas na representação simbólica aumenta duas unidades o “Number Bond”. Assim, a criança tem de estar atenta, analisar a variedade de situações inter-ligadas e estabelecer relações entre o concreto e o abstrato e tirar as suas conclusões.
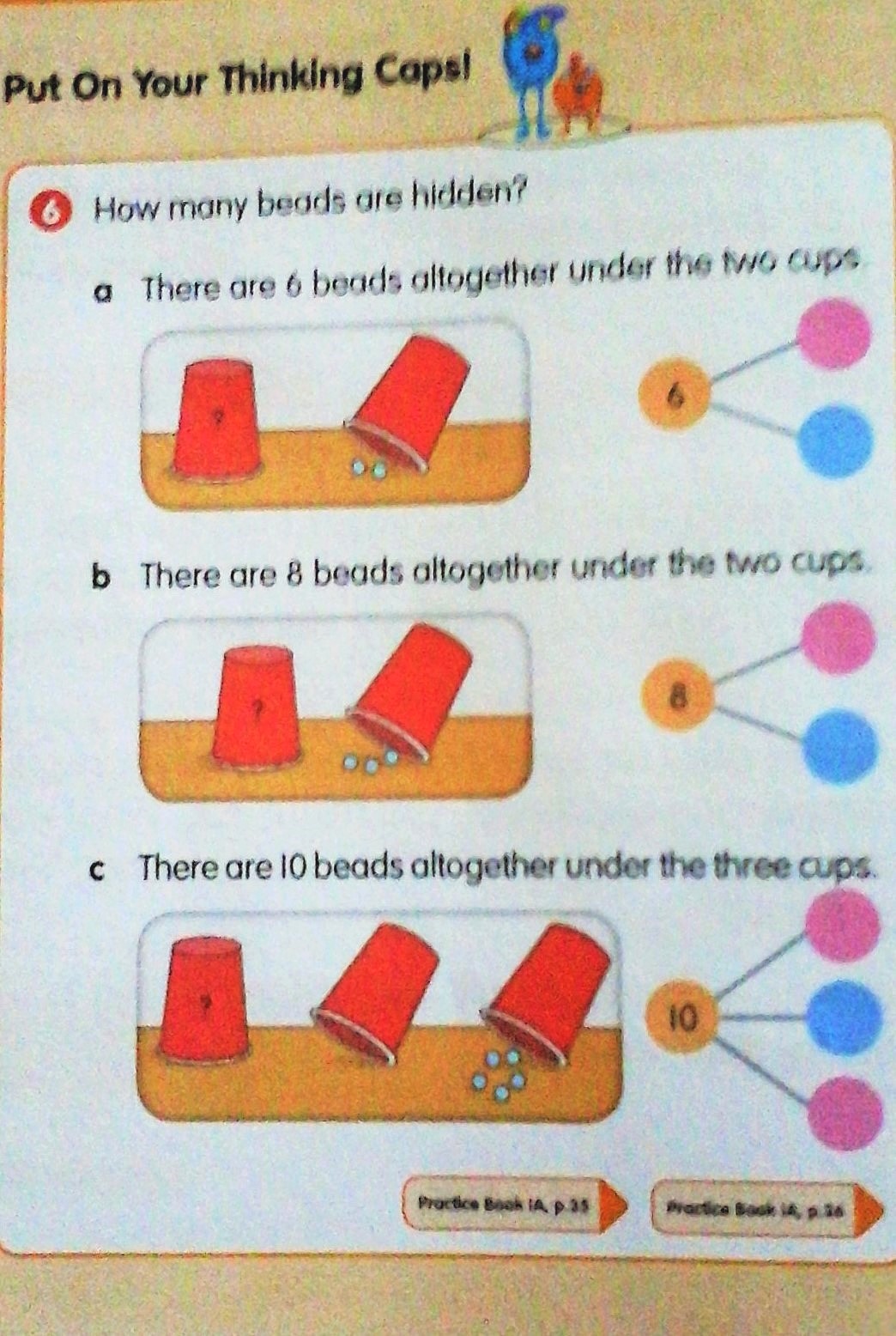
Figura 2: Atividade lúdica da noção de “Number Bond”, usando dois ou três ramos.
Na atividade anterior é proposto à criança a exploração do “Number Bond” com dois ou três baldinhos com berlindes para concretizar a situação. O estudante observa e/ou concretiza, contando a quantidade de berlindes sob um dos baldinhos, precisando de identificar a quantidade de berlindes que deve ter sob o outro baldinho para compor o número que seja o “todo”. Note-se ainda o caso particular do uso do número “0” no item três, em que não há nenhum berlinde sob o baldinho do meio. Este tipo de tarefas de natureza lúdica preconizam o desenvolvimento do pensamento pré-algébrico, relacionado com a necessidade de abstrair, aproximando-se do conceito de incógnita a explorar nas equações do 2.º ciclo.
Como se referiu anteriormente no desenvolvimento do sentido de número devem ser explorados diferentes materiais, como materiais da vida real, cubos de cor, balanças numéricas, material de tipo Cuisenaire, molduras do 6, 8 e 10, Material Arithmetic Basic ou peças multibásicas de base 10, pois favorecem a construção diferenciada de quantidades, bem como o design gráfico do “Number Bond”. Convém recordar que a (de)composição dos números elementares, das quantidades até 10 e depois até 20 é crucial no desenvolvimento do cálculo mental. Esta abordagem, felizmente, já era usada em Portugal por muitos professores, mas numa representação horizontal e não com este aspeto gráfico exposto na figura anterior ou nas figuras seguintes, figuras 3 e 4, respetivamente, usando diferentes materiais: balança numérica e/ou os cubos de cores.
Figura 3: Balança numérica e “Number Bond” (NB).
No exemplo da figura 4, propõe-se o uso dos cubos de cor e/ou da balança numérica para se construir o “NB” 9, usando três ramos e três soluções. No exercício 2 desafia-se ainda o estudante para descobrir mais de duas soluções no caso do 10.
Figura 4: “Number Bond” 9 e 10, usando 3 ramos e várias soluções.
Na noção do “Number Bond” o número representado no lado esquerdo (o todo) é decomposto em partes (neste caso em três), para generalizar a ideia de parte-todo e de comparação. Registe-se que para além da balança utiliza-se o material concreto (cubos de cor) para conectar a compreensão anterior da representação de um número e fortificar a contagem de quantidades. Este estudo do todo e das partes, usando os cubos de cor ou outros materiais preparam a ideia de modelagem por barras (“Modeling Bar” ou “Bar Model”) e que será explorado neste artigo num dos pontos seguintes.
De reparar ainda que o esquema do “Number Bond” também vai ser usado com outras operações, como mostra a figura 5 a explorar posteriormente.
Figura 5: Esquema do “Number Bond” a ser usado na adição e na multiplicação.
Outra aplicação concreta é apresentada na figura 6, existente na internet (wikihow.com) na qual se utiliza o “Number Bond” 15 e 24 numa decomposição mais generosa para a adição, permitindo agilizar os cálculos.
Figura 6: Aplicação do “Number Bond” (NB) à adição, agilizando os cálculos.
O “NB” vai acompanhar todo este processo de aprendizagem do número e das quatro operações aritméticas: adição, subtração, multiplicação e divisão. O mais importante é analisar cada situação e descobrir a decomposição mais conveniente para agilizar o processo operatório e desenvolver o cálculo mental.
3. Exploração do “Basic Fact Family” (BFF) ou “Fact Family Numbers” (FFN)
Uma das noções também trabalhadas logo desde o 1.º ano de escolaridade é a de “Fact Family Numbers”. Trata-se de explorar um terno de números que fazem sentido para a adição e a subtração, relacionando-os. Deste modo, na resolução de problemas relaciona-se a adição e a subtração nos chamados “Basic Fact Family” de 3 números. Por exemplo, no caso do “Basic Fact Family” de 2,7, 9 (Figura 7) traduz-se nas expressões seguintes, usando a adição e a subtração. Numa 1.ª fase devem-se usar os cubos de encaixe para a criança concretizar e compreender melhor a situação problemática, realizando o design pictorial pelo “Bar Model” que deve anteceder a representação simbólica que a seguir se expõe.
Figura 7: “Fact Family Numbers” ou “Basic Fact Family” do 2, 7 e 9, nas operações lineares.
Nesta sequência devem-se realizar vários exemplos do “Basic Fact Family”, usando três números que podem ser propostos pelo professor ou criados pelas crianças, como: 7, 8 e 15. Neste tipo de tarefa devem ser exploradas todas as hipóteses existentes, isto é, as quatro possibilidades de relacionar os três números usando a adição e a subtração.
Naturalmente que o “Fact Family Numbers” (FFN) vai ser usado nas quatro operações aritméticas, reconhecendo-se que existem sempre quatro soluções para a adição e a subtração assim como para o caso da multiplicação e da divisão inteira exata. A figura 8 mostra um exemplo deste conceito, apesar de ser de uma forma incompleta, dado que no FFN ao relacionar duas operações existem sempre quatro soluções. No caso do terno: 7, 3 e 4 faltam as soluções: 7-4=3 e 4+3=7 e no caso do terno: 2,4 e 8 faltam as soluções: 4x2=8 e 8:2=4.
Figura 8: “Fact Family Numbers” usados nas quatro operações.
Como se referiu o “Number Bond” vai acompanhar os cálculos das diversas operações, mas no caso da “Fact Family Numbers” a decomposição tem de estar relacionada com duas operações de cada vez, com a adição e a subtração ou noutro caso com a multiplicação e a divisão, como mostra a figura 9. No caso dos valores: 6, 3 e 18, os FFN que se apresentam relacionam a multiplicação com a operação inversa, a divisão inteira exata.
Figura 9: “Fact Family Numbers” (FFN) com a multiplicação e a divisão.
Podem-se ainda descobrir variantes com outros grafismos: “Basic Fact Family in triangle”. Assim, com base na imagem de um triângulo, escreve-se o valor numérico em cada vértice, bem como a(s) respetiva(s) operação(ões) associadas. Por exemplo, no caso anterior colocar-se-ia o 9 num vértice e as duas operações: 2+7 ou 7+2; no outro vértice o 7 e a operação 9-2 e no outro vértice do triângulo o 2 e a operação 9-7.
4. “Modeling Bar”, “Bar Model” ou “Modelo de Barras”
O “Modeling Bar” ou “Bar Model” é usualmente explorado na resolução de problemas. Reconhece-se ainda que este tipo de representação vai, sem dúvida, suportar a aprendizagem da Álgebra que é a linguagem mais abstrata no domínio da Matemática. As crianças revelam normalmente sérias dificuldades na aprendizagem deste tópico, existindo por vezes, um abandono precoce à disciplina, devido à complexidade deste domínio. Assim, ao usar-se o “Modeling Bar” na resolução dos problemas, como se indica na figura seguinte (figura 10), vai ser possível suportar uma aprendizagem da pré-álgebra que facilitará a compreensão dos conteúdos a serem lecionados no 2.º ciclo do ensino básico. Nesta perspetiva vale a pena pensar nesta estratégia de modelação como uma aprendizagem formativa e gradual da Álgebra. A análise dos exemplos seguintes permite-nos descobrir a importância desta representação na leitura, interpretação e compreensão do problema diretamente relacionados com a adição e a subtração.
Figura 10: “Bar Model” na resolução de problemas.
No exemplo seguinte (figura 11) são usados, na Prática Orientada (Guided Practice), os passos necessários para a criança ler, interpretar a informação e registar as suas conclusões. Neste processo é crucial que a criança siga “religiosamente” “step by step” o esquema da resolução de cada problema para pensar, analisar, compreender e generalizar.
Figura 11: Explicação prática do “Bar Model”.
No exemplo da figura 12 apresenta-se a resolução de mais um problema em que se usa o “Bar Model” para a crianças ser capaz de relacionar melhor a informação e concluir de forma correta a resolução do problema.
Figura 12: Explicação prática do “Bar Model” na resolução de um problema.
Apesar de se ter apresentado primeiro a funcionalidade da exploração do “Bar Model” (BM) na resolução de problemas anteriores, a evolução inicial da construção gradual do uso do “BM” passa naturalmente pelo que está exposto na figura 13 e posteriormente na figura 14. Assim, na tarefa da figura 13 apela-se ao “companheirinho” da representação pictórica das pecinhas no quadro, com base num número reduzido de “cubinhos”. No segundo quadro aumenta um pouco a quantidade representada. E no terceiro quadro surge um dilema, pois a quantidade é muito grande e o desenho dos “quadradinhos” correspondentes não cabe no quadro. Deste modo, a criança vê-se confrontada com uma situação que não sabe como resolver.
Figura 13: Processo progressivo da construção do “Bar Model”.
Nesta utilização do “Modelo de Barras”, em que se concretiza com cubos de cor, Dotti (2016) defende que a solução descoberta generaliza o conceito de representação pictórica, em que a ideia que se abstrai é a quantidade e não a peça concreta. A barra representa o número que corresponde à quantidade de peças, ocorrendo, assim, a passagem do concreto para a representação pictórica. Ao trocar a representação das pecinhas pela barra, o estudante faz uma representação pictórica de uma quantidade apresentada no material concreto. Por outro lado, ao usar a barra (sem partições) para representar uma quantidade, é feita a generalização, ou seja, o estudante deve compreender que dentro do espaço disponível para desenhar, ele pode usar uma barra (de qualquer tamanho e que não precisa ser dividida em unidades) para representar qualquer quantidade. Todo este processo de representação pictórica e generalização é um sistema de abstração que a criança concretiza e deve vivenciar, do mais simples ao mais complexo, integrando sempre as fases da exploração anterior. Além disso, o estudante associa o tamanho da barra à quantidade que ela representa, como se mostra na imagem do último quadro com o 20 e o 4 (figura anterior 13). Consequentemente, ao fazer associações, representações, generalizações e abstrações, o estudante está a desenvolver o pensamento algébrico.
Deste modo, para resolver uma situação problema o estudante precisa de escolher a estratégia mais adequada para chegar ao resultado, mas nesse processo necessita de saber identificar e interpretar os dados do problema. O “Modelo de Barras” é um recurso didático que facilita esta escolha, pois através do modelo o estudante faz a representação pictórica dos dados e a interpretação dos mesmos permite a modelagem do problema. Além disso, o registo desses dados e as suas interpretações são a base para argumentar e justificar as escolhas das operações assim como para validação da resposta final.
O exemplo seguinte (figura 14) e num primeiro enunciado: “Googol assou 10 biscoitos de gengibre. Aida assou 12 biscoitos de gengibre. Quantos biscoitos de gengibre assaram os dois, no total?, ao utilizar-se o “Bar Model” aprende-se a compreender o problema, concretizando-se e modelando-se a situação como um todo. O mesmo acontece no enunciado do segundo problema (2).
Figura 14: Problemas com “Bar Model” usando a adição.
O professor deve trabalhar com detalhe e de modo assíduo este modelo na classe, pois é a representação pictórica correta feita pelo estudante que proporciona a compreensão dos dados do problema. O reconhecimento mental da similitude entre a representação feita pelo material concreto e pela barra deve ocorrer na etapa da representação pictórica. Na figura anterior (figura 14) observam-se duas barras que correspondem respetivamente à quantidade de biscoitos assados por Googol e Aida. O desenho de unir as duas barras representa a compreensão da condição contida na pergunta do problema: “juntos”, ou o “todo”, no significado de “acrescentar” da adição.
O “Modelo de Barras” (MB) permite que o estudante tenha uma visão integral do problema e reforce conceitos básicos da matemática, por meio dos significados das operações. Este tipo de representação mostra-se ainda muito útil na compreensão das propriedades aritméticas, que auxilia na transição do concreto para o abstrato, ou seja, através da representação pictórica pelo MB o estudante consegue progredir da utilização de materiais concretos para expressar-se na linguagem matemática abstrata, e tudo indica que isso permitirá obter êxito na transição da aritmética para a álgebra nos anos seguintes.
Ao utilizar-se o “MB” como método de representação pictórica de situações problema é importante reforçar a necessidade do professor colocar questões apropriadas ao estudante sobre o que está acontecendo em cada momento da resolução para promover processos de metacognição, de pensar sobre o seu próprio pensamento. O professor deve conduzir a aula de modo que o próprio estudante seja capaz de explicar como fez e porque fez de determinada maneira. A resolução de problemas como estratégia de aprendizagem gradual e integrada permite que, posteriormente, o estudante tenha competência para modelar outros problemas idênticos.
5. Adição em ação
A adição deve ser desenvolvida com base na resolução de um problema da vida real da criança como por exemplo no caso já apresentado na parte I deste artigo das jarras de flores. Inicialmente deve ser proposto o trabalho com duas parcelas, posteriormente com três ou mais e numa primeira fase com os números elementares: do 1 ao 5, depois até ao 10, seguindo-se até ao 20. Só depois de serem desenvolvidos problemas com estas quantidades se deve avançar para quantidades superiores: até 40 ou 50 e por fim até ao 100, no 1º ano de escolaridade.
Como se referiu anteriormente o grafismo do “Number Bond” e do “Bar Model” está naturalmente associado à resolução dos problemas de adição e das outras operações aritméticas. Na figura seguinte (figura 15) mostram-se exemplos com números elementares e com quantidades até ao 20, relacionados com a utilização deste método na adição, numa perspetiva de desenvolvimento do cálculo mental o qual deve anteceder o ensino do algoritmo.
Figura 15: Uso do “Bar Model” e do “Number Bond”, com “os amigos do 10”.
No exemplo seguinte (figura 16) surge a motivação através da questão problema relacionado com a decomposição de quantidades tendo por base o Material Arithmetic Basic (as peças multibásicas de base 10) em que a criança tem de reconhecer quantidades, manipulá-las e representá-las simbolicamente. Todo este tipo de trabalho pressupõe o conhecimento do sistema de numeração posicional decimal, a decomposição de quantidades e a construção do “Number Bond”, que sustenta o desenvolvimento do cálculo mental.
Figura 16: Decomposição de quantidades relacionadas com a adição.
Na figura 17 propõe-se a resolução de um problema com quantidades superiores a 20, em que a primeira parcela é superior a 20 e a segunda é um número elementar. Coloca-se a situação problemática em destaque e exploram-se as diversas estratégias de resolução criadas pelas crianças ou as que se mostram na imagem. Na “activity time” é proposta uma tarefa para ser realizada aos pares e ainda a Prática Orientada (Guided Practice), usando o “Number Bond”.
Figura 17: Adição entre 20 e 40 com diversos métodos, inclusive o algoritmo.
Os exemplos que se apresentam de seguida, procuram estimular o desenvolvimento do cálculo mental, relacionando a adição com a subtração e usando a noção de “Number Bond”.
Figura 18: Aplicação do “Number Bond” no cálculo de somas e diferenças.
Nestas atividades os estudantes trabalham o cálculo mental, resgatando e ampliando as atividades anteriores de decomposição de números em suas partes. Para facilitar a aprendizagem da técnica de cálculo mental, as operações resolvidas inicialmente são de adição, em que uma das parcelas tem valor menor que 10, conjugando a adição com a subtração, mas com aproximações à dezena.
Outros exemplos são explorados de modo que a criança se sinta confortável na aplicação deste método para posteriormente ser ensinado a técnica do algoritmo da adição. Esta tem a ver com a estrutura similar à usada em Portugal, como mostram as imagens seguintes, sendo concretizadas no modelo CPA e com o apoio das peças multibásicas de base 10 (MAB).
Figura 19: Estrutura do algoritmo da adição sem reagrupamento “sem transporte”.
De reparar que na figura anterior, a imagem do lado direito deve ser a usada, pois não há “traços” verticais a separar as ordens e, assim, o número é tratado como um todo, como convém. Contudo, seria de todo conveniente ser desenhado um “traço” horizontal para separar a indicação das ordens dos algarismos que constituem as duas parcelas.
A estrutura do algoritmo da adição por reagrupamento, vulgarmente chamado em Portugal de adição “com transporte”, é explorada de forma diferente em Singapura. Assim, antes de se ensinar a técnica é desenvolvida, com gradualidade o ensino da mesma, como mostra a figura seguinte (figura 20): numa primeira fase usa-se o método das somas parciais, para na reta final se usar uma técnica e um grafismo similar ao desenhado em Portugal (figura 21).
Figura 20: Estrutura do algoritmo da adição com reagrupamento em Singapura.
Com base no exemplo anterior e na fase final da apresentação da técnica do algoritmo, em Singapura, procede-se do seguinte modo: adiciona-se 4 com 7 que dá 11 unidades ou 1 dezena e 1 unidade e então diz-se “e vai um” ou “vai uma dezena” e dois com mais uma dezena que “vem de trás” soma 3 e colocar-se-ia 3 na ordem das dezenas. O resultado final de 24 com 7 seria 31 (24+7=31) e a estrutura usada é idêntica à usada em Portugal (um exemplo na figura 21).
Figura 21: Estrutura do algoritmo da adição com reagrupamento “com transporte”.
Em Singapura, como se referiu na figura anterior, existe uma evolução até chegar ao ensino do algoritmo e nesse trajeto são trabalhados outros métodos como os que a seguir se apresentam e explicados na figura 22.
Figura 22: Métodos da adição usados em Singapura antes do método tradicional.
É curioso registar que o primeiro algoritmo da figura 21, desenvolve-se da direita para a esquerda: 1.º adicionam-se as unidades, depois as dezenas e por último as centenas. Por fim determina-se o total, adicionando-se sempre no mesmo sentido. Em termos históricos este método já era conhecido e usado na idade média e chama-se o “método das somas parciais”.
Para uma melhor compreensão da aprendizagem do algoritmo da adição, sem e com reagrupamento, é necessário ser usado o Material Arithmetic Basic (MAB), no qual os “cubinhos” representam as Unidades, as “barras” as Dezenas e as “placas” as Centenas. Numa fase posterior pode-se usar o ábaco vertical (em que as peças das diferentes ordens têm a mesma cor), como mostra a figura seguinte (figura 23), para realizar cálculos de somas e mais tarde de diferenças.
Figura 23: Uso do ábaco vertical no cálculo de somas e na aprendizagem do algoritmo.
Naturalmente que o algoritmo tem de ser trabalhado de diversas formas e com vários materiais, relacionando-os, principalmente, com a resolução de problemas, como se mostra nas imagens seguintes da figura 24.
ou
Figura 24: Prática Orientada do algoritmo da adição.
A criança deve ser estimulada a utilizar os vários processos que foram apresentados anteriormente para que saiba selecionar o método mais adequado a cada situação e aprofundar, assim, o conhecimento da adição.
6. Subtração em ação
Para se trabalhar qualquer operação tem de se perceber o conceito, conhecer as propriedades e os significados associados. Contudo, se a adição tem dois significados: “acrescentar” ou “juntar” e “combinar”, a subtração tem três: “retirar”, “completar” e “comparar” e é por isso que o resultado da subtração pode ter três designações, respetivamente, “resto”, “excesso” ou “diferença”. Estes aspetos concetuais têm de ser conhecidos para que cada operação seja trabalhada da forma mais completa e correta possível, pois quanto mais se sabe matemática melhor é o professor! E esta máxima é o eixo estruturante da Matemática ensinada em Singapura (e eu diria em qualquer país)!
Ora, tem de se reconhecer que cada um dos significados tem a sua conceção, linguagem e a adequação na exploração didática!
Assim, tal como na abordagem de outras operações, a subtração inicia-se com a apresentação de um problema de palavras e o uso de objetos concretos. Neste caso deve-se começar com o significado de “retirar”, pois é o mais simples. Apresenta-se oralmente e/ou por escrito um problema semelhante a: Na mesa havia 8 laranjas. O Jorge comeu 2 laranjas. Quantas laranjas ficaram na mesa?
Nesta sequência debate-se oralmente o problema para se perceber bem a mensagem. Depois deve-se representar graficamente a situação, usando “círculos” alaranjados no quadro e numa folha de papel, numa representação coletiva e individual da situação.
De seguida deve-se escrever uma expressão numérica que simbolize matematicamente a situação, usando os algarismos e símbolos adequados: “8-2=6”.
Quando se trabalha a subtração deve ser associada, no momento adequado, à adição como operação inversa e serem apresentados os “Fact Family Numbers”, como acontece com o terno: 10, 7 e 3.
Figura 25: “Fact Family Numbers” do 10, 7 e 3.
Claro que a relação entre estes três dados numéricos relacionando a adição com a subtração, evidencia uma das propriedades da subtração - a propriedade fundamental da subtração - o aditivo é igual à soma do subtrativo com o resto, excesso ou diferença. Esta deve ser bem trabalhada pelas crianças para validar o resultado correto da subtração, relacionando-a com a adição. Por outro lado, este conjunto de factos, pelo uso de duas adições e duas subtrações, deve ser associado a problemas a serem inventados pelas crianças.
É importante que as crianças façam desenhos para representar os problemas propostos e resolvem-nos de forma diversa, apresentando estratégias pessoais de cálculo diferentes.
Por outro lado, antes de prosseguir para outras quantidades superiores o professor deve ter a certeza que os estudantes entenderam plenamente os diferentes situações e resoluções apresentadas.
Quando o professor considerar conveniente devem ser abordados os outros significados da subtração, como no caso de completar: “Numa mesa existem 9 laranjas e 5 perras. Quantas peras são necessárias colocar na mesa para ter o mesmo número de laranjas?” e de comparar: “Numa sala existem 15 raparigas e 11 rapazes. Quantas raparigas há a mais do que rapazes?”
Deste modo, nos exemplos seguintes (figura 26 e figura 27) são propostos problemas cuja resolução está associada ao “Modeling Bar” ou ao “Number Bond” (figura 27) e só depois é que surge o ensino da técnica do algoritmo da subtração.
A proposta de resolução do problema: a Amy tem 12 brinquedos e o Ben tem 8. Quantos brinquedos tem a mais a Amy do que o Ben? tem a ver com o esquema do “modeling bar” (figura 25). A resolução do mesmo apresenta-se diretamente relacionado com a subtração e com a expressão matemática: “12-8=4”.
Figura 26: “Modeling Bar” diretamente relacionado com a subtração
Figura 27: Resolução de problemas da subtração usando materiais concretos: cubos de cor, o “Modeling Bar” e o algoritmo.
No exemplo seguinte (figura 28) são apresentadas diferentes estratégias de resolução de um problema usando a contagem regressiva, o material MAB, a noção de “Number Bond” e também o algoritmo.
Figura 28: Diversos métodos usados no cálculo de diferenças.
O ensino do algoritmo sem reagrupamento é idêntico ao da adição, como se percebe do exemplo seguinte (figura 29). Contudo, na subtração com reagrupamento, “com transporte” em Singapura usa-se o método da decomposição do aditivo. Este método também é usado há bastante tempo, e com muito êxito, por muitos professores portugueses.
Figura 29: Esquemas do algoritmo da subtração sem reagrupamento.
Tal como na adição também no algoritmo da subtração tem de se ter em conta as observações referidas para uma representação mais rigorosa no ensino do algoritmo destas duas operações e a apresentação da técnica (figura 30).
Figura 30: Esquemas de representação do algoritmo da subtração com reagrupamento.
Repare-se que no exemplo anterior no cálculo de 35-16, o aditivo é decomposto em 20+15, isto é, 35=20+15. Assim, já é possível subtrair 6 a 15 e realizar a subtração. O ensino do algoritmo com reagrupamento, em Singapura, é baseado nesta decomposição do aditivo e no uso do material de peças multibásicas de base 10 (MAB) para a criança compreender os procedimentos.
De facto, existe outro método para o ensino desta temática usado em Portugal, mas este é o mais lógico, o mais acessível e o mais compreendido pela criança.
7. Reflexões finais
Na senda do ensino da Matemática em Singapura têm-se realizado várias reflexões sobre como fazer ciência matemática no “Ensino Primário”. Neste 1.º Ciclo do Ensino Básico os professores também são professores de Matemática e este período é determinante para a criança vir a gostar ou não desta disciplina! Através desta pesquisa é possível perceber como é importante o professor saber Matemática, adquirir conhecimento sobre Didática, aplicar esses saberes na sala de aula, estudando e usando vários métodos: CPA, “Number Bond”; “Modeling Bar” (“Modelo de Barras”); “Fact Family Numbers”, ….) e perceber por que razão se faz isto e não aquilo! Tudo tem o seu propósito, a sua intencionalidade, como por exemplo o “Modelo de Barras” vai contribuir para o desenvolvimento do raciocínio algébrico da criança.
A Matemática de Singapura desenvolve nos estudantes a capacidade de analisar as informações, de visualizar as situações problema através da modelagem, de reconhecer padrões e fazer generalizações, e de desenvolver competências de manipulação numérica através do cálculo mental. Além de se focar nas relações de parte-todo e comparação, a visualização pictórica favorece a transição do concreto para o abstrato através da resolução de problemas, de cariz essencialmente algébrica. Por outro lado, os conceitos são ensinados lentamente, porém com profundidade, permitindo que os estudantes progridam de forma sustentada no desenvolvimento das suas capacidades essenciais da aprendizagem da matemática.
Também é possível entender que não é apenas uma metodologia que suporta o sucesso para aprendizagem de determinados conteúdos, mas uma proposta curricular que faça sentido para a criança e com consistência didática, em que o objetivo de aprendizagem pode ser seguido continuamente ao longo de uma sequência didática coerente.
Ao analisar a estrutura associada ao ato de pensar e ensinar Matemática em Singapura faz sentido aprofundar este saber para se perceber que ao existir uma sequência de tarefas e materiais apropriados, com atividades coerentes é possível orientar os estudantes a pensar, a refletir, a conjeturar, a validar hipóteses e a tirar conclusões, desenvolvendo poderosos mecanismos de metacognição. Só assim é imaginável aprender com gosto a Matemática.
Algumas Referências
Dotti, Tamara G. P. (
2016). Um estudo do Modelo de Barras nos livros didáticos da matemática de Singapura: fundamentação da Álgebra no ensino Fundamental 1.º Ciclo. São Carlos: Universidade Federal de São Carlos.Fernandes, D. (1994). Educação Matemática no 1º ciclo do ensino básico. Porto: Porto Editora
Fernandes, D. (2006). “Aprendizagens algébricas em contexto interdisciplinar no ensino básico”. Tese de Doutoramento não publicada, Universidade de Aveiro, Aveiro, Portugal.
Fernandes, D. (2017). Sendas de Sucesso com o “método de Singapura” – Parte 1. Publicação on-line na revista OZARFAXINARS nº 70. http://www.cfaematosinhos.eu/ozarfaxinars.htm).
Har, Bean YY. (2017). Apontamentos de formação sobre o projeto “mathsnoproblem” – Singapoure maths. Londres.
NCTM (2007). Princípios e normas para a Matemática escolar. Lisboa: APM.
Piaget, J. (1975). A formação do símbolo na Criança. (2ª edição). Rio de Janeiro: Zahar Editores/MEC.
PISA (2012). Results in Focus What 15-year-olds know and what they can do with what they know. In Gurría, A. (Ed.). Report OECD 2014.
Ramakrishman, C. e Wah, B. (2015). INSPIRE MATHS. ASSESSMENT BOOK 1. Kheong, F. (Consultant and Author of Singapore Maths). Skinner, C. ; D´Angelo, S. e Gibbs, E. (UK consultants). Oxford: OXFORD University Press.
Ramakrishman, C. e Wah, B. (2015). INSPIRE MATHS. PRACTICE BOOK 1A. Kheong, F. (Consultant and Author). Skinner, C. ; D´Angelo, S. e Gibbs, E. (UK consultants). Oxford: OXFORD University Press.
Ramakrishman, C. e Wah, B. (2015). INSPIRE MATHS. PRACTICE BOOK 1B. Kheong, F. (Consultant and Author). Skinner, C. ; D´Angelo, S. e Gibbs, E. (UK consultants). Oxford: OXFORD University Press.
Ramakrishman, C. e Wah, B. (2015). INSPIRE MATHS. PUPIL TEXTBOOK 1A. Kheong, F. (Consultant and Author). Skinner, C. ; D´Angelo, S. e Gibbs, E. (UK consultants). Oxford: OXFORD University Press.
Ramakrishman, C. e Wah, B. (2015). INSPIRE MATHS. TEACHER´S GUIDE 1A. Kheong, F. (Consultant and Author). Skinner, C. ; D´Angelo, S. e Gibbs, E. (UK consultants). Oxford: OXFORD University Press.
Site: http://pt.wikihow.com/Ensinar-a-Matem%C3%A1tica-de-Cingapura
OZARFAXINARS nº 70: http://www.cfaematosinhos.eu/ozarfaxinars.htm.
https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
http://community.ksde.org/LinkClick.aspx?fileticket=n2ZHaEprrfs%3D&tabid=6036&mid=14879
http:// www. wikihow.com
Nota curricular da autora
Dárida Maria Fernandes é Professora é Coordenadora da Unidade Técnico-Científica de Matemática, Ciências Naturais e Tecnologias da Escola Superior de Educação do Politécnico do Porto. Doutorada em Didática pela Universidade de Aveiro, Mestre em Educação na especialidade de Tecnologias de Informação pela Universidade do Minho. Licenciada em Matemática – Ramo Educacional pela Faculdade de Ciências da Universidade do Porto e Bacharel pela conclusão do Curso do Magistério Primário do Porto. Experiência profissional vasta no ensino da Matemática, desde o 1.º Ciclo do Ensino Básico (7 anos), no Ensino Básico e Secundário (3 anos) e no Ensino Superior (28 anos) relacionada com a formação de educadores e professores. Membro do Conselho Técnico-Científico por inerência de categoria profissional, desde 1989 e posteriormente por eleição, desde 2010, tendo assumido a responsabilidade de vários cargos de gestão intermédia na ESEPP. É responsável por Unidades Curriculares de Matemática e Ensino da Matemática relacionadas com a formação de Educadores de Infância e de Professores do 1.º e 2.º Ciclo do Ensino Básico (CEB) e pela Supervisão na Prática de Ensino Supervisionada de professores do 1.º e 2.º CEB. Participação em júris de seleção e seriação de candidatos para os mestrados profissionalizantes, participação em júris de mestrado e de doutoramento em outras instituições. Participação ativa em congressos nacionais e internacionais, com apresentação de comunicações individuais ou em grupo, resultantes de trabalhos de investigação realizados sobre várias temáticas, designadamente sobre o ensino da Álgebra em contexto interdisciplinar em aprendizagens formais e não formais, formação inicial e contínua de professores. Coordenadora do mestrado em ensino do 1.º e 2.º CEB e do atual mestrado em ensino do 1.º CEB e em Matemática e Ciências Naturais do 2.º CEB. Coordenadora de diversos projetos relacionados com o ensino da Matemática: “Baú de Matemática” (9 anos); “Envolvências Geométricas I e II – A Geometria na Cidade” (4 anos), patrocinados pelo programa Ciência Viva, bem como do “Divertir com o saber”, uma parceria com a Câmara Municipal de Vila Nova de Gaia (11 anos). Coordenadora de várias formações no âmbito da Matemática e do Ensino da Matemática, designadamente, do Programa de Formação Contínua de Professores do 1.º e 2.º CEB, de iniciativa Ministerial, durante 6 anos de vigência do mesmo. Professora e colaboradora na área de Matemática em várias universidades europeias, designadamente, em França, Inglaterra, Estónia, Espanha, Eslovénia, Holanda, Hungria, entre outras, resultante de parcerias institucionais e de um projeto de formação de professores do “Ensino Primário”, a nível europeu, designado por EPTE (European Primary Teachers Education). Leader na ESEPP, de 2012 a 2015, do programa PAEDEIA onde estiveram envolvidos cinco países: Dinamarca, Finlândia, Suécia, Turquia e Portugal, relacionado com o programa de indução. Conferencista em vários congressos nacionais e internacionais por proposta ou convite como Keynote Speaker na área de Matemática e Ensino desta disciplina. Autora de manuais para o 1.º CEB e de roteiros para inovar práticas nesta disciplina, bem como de livros para professores e artigos publicados em revistas ou livros de referência. Formadora responsável de diversas ações de formação, de sua iniciativa ou em colaboração com outros formadores para centros de formação, instituições de solidariedade social ou outras. Consultora de Matemática em várias instituições, desenvolvendo projetos inovadores, sendo um deles relacionado com a implementação do “método de Singapura” e do “math daily 3” em desenvolvimento no 1.º Ciclo do Ensino Básico.
No ano letivo, 2017-18, exercerá funções de formadora no CFAE_Matosinhos, no âmbito do PNPSE - Programa Nacional de Promoção do Sucesso Escolar, enquadrado em protocolo estabelecido entre a ESEP - Escola Superior de Educação do Porto e o CFAE_Matosinhos.
Agradecemos, desde já, a sua opinião sobre este número - ozarfaxinars@gmail.com
© CFAE_Matosinhos